【思路】

这个是一个非常容易看出来的模拟，但是模拟也是有技巧的

一般人的模拟思路一般就是移动元素或者下标

然后我就看到了一个有趣的思路

建立坐标轴

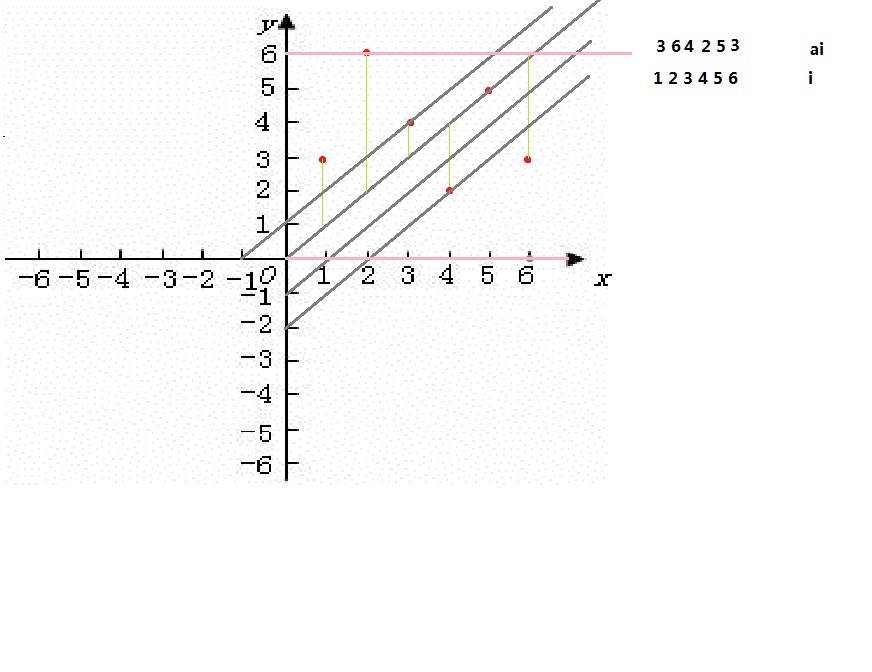
以i坐标为横坐标，以si为纵坐标，然后画一条斜率为1的直线，当y=x时，每个点到这条直线的竖直距离就是最开始没有旋转操作的值

 

如上图，我自己手写一组数据，然后画了一个图，绿色的细线的总长就是没有进行操作时的答案 

然后我们就来对这组数据进行操作，我们可以将这条直线左右平移，向左平移的时候，第1到第n-1个点的计算方式还是到直线的竖直距离，不过第n个点的计算方式不一样了

而向右平移，就是2到n点计算方式不变，第一个有变

刚刚那句话的正确性可以根据这张图来证明

然后我的做法是将直线左移，每次下标为n的点要特殊处理，其他点就是在移之前是在直线上方的是减去一个价值，而刚刚在直线上和直线下方的是加上一个价值，

然后只需要处理移动后点和直线的位置关系就行

1 #include
      
        2 #include
       
         3 #include
        
          4 #include
         
           5 #include
          
            6 #include
           
             7 #include
            
              8 #define LL long long 9 #define maxn 1000510 using namespace std;11 12 int tmp,ans,n,up,down;13 int num[maxn],a[maxn],cnt[maxn];14 15 int read(){16 int x=0,f=1;char ch=getchar();17 while(ch<'0'||ch>'9'){ if(ch=='-')f=-1;ch=getchar();}18 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}19 return x*f;20 }21 int main(){22 n=read();23 for(int i=1;i<=n;i++){24 a[i]=read();25 if(a[i]>i)tmp+=a[i]-i,cnt[a[i]-i]++,up++;26 else tmp+=i-a[i],down++;27 }ans=tmp;28 for(int i=1;i<=n;i++){29 tmp+=down-up;30 tmp-=n+1-a[n-i+1];31 tmp+=a[n-i+1]-1;32 down--;33 if(a[n-i+1]>1)up++,cnt[i+a[n-i+1]-1]++;34 else down++;35 up-=cnt[i];down+=cnt[i];36 ans=min(ans,tmp);37 } 38 cout<